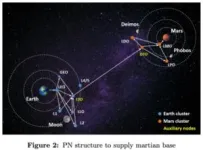
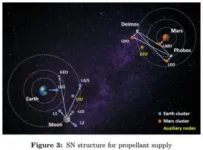
First of all, the problem scope and the theoretical foundation are presented. The considered ISC network is a layered network in which nodes represent points of interactions between the two layers. The two interacting networks are PN which delivers cargo from Earth to Mars and SN that is responsible for the propellant supply along the way, respectively. They share the same nodes but comprise different arcs based on their distinct purposes. The nodes are defined as surface nodes (celestial bodies where supplies and demands are generated), orbital nodes (relatively stable orbits accessible from surface nodes), Lagrange points (potential positions for on-orbit infrastructure), and auxiliary nodes (LTO and DTO which serve as the gateway for inter-cluster travel). Propellant Consumption is given by a propellant mass fraction which is directly derived from the rocket equation.
Then, the author formulates Multi-Stage Stochastic Programming (MSP) modeling. The proposed MSP model for ISC planning considers demands at a Martian base as a source of uncertainty. Uncertainty is represented through random variables, which follow specified probability distributions. And, a scenario set which essentially constitutes a discrete approximation of the original probability distribution enables MSP to reflect uncertainty at multiple points in time. Two classes of decision variables are also differentiated in the developed MSP model: strategic scenario-independent variables, which represent decisions that have to be made before the uncertainty unfolds and cannot be altered over the course of the planning horizon, and tactical scenario-dependent variables, which are made after the uncertain parameters have materialized and can be adjusted over time. Based on the above model description, a multi-stage stochastic MILP model is developed, in which the objective function shown in Eq. (3) minimizes the total launch mass (TLM).
(3)
The flows of spacecraft, payload, and propellant in the PN, the propellant flows in the SN, and other constraints are stated in detail as well.
Afterwards, numerical studies are discussed. In the optimization, the considered planning horizon comprises 6 years (on Earth) divided in 24 periods of 3 months each. The demands are assumed to be a seasonal pattern, affected by the quite harsh seasonal conditions on Mars, and do not occur before period 9. Based on the approach used by Hahn and Kuhn [20], seasonal demands for each period and scenario are calculated as shown in Eq. (22), in which the scenario factor ft,s is to generate the number of scenarios from the baseline case, the base level of demand is estimated at dibase=50 t for i=Mars, and remaining terms generates the seasonal demand pattern from the demand base level by assuming a harmonic oscillation with an amplitude of amp=0.1.
To account for uncertainty in models, a discrete set of scenarios are generated, each of which comprises discrete realizations of every uncertain parameter, which is captured in the scenario factor ft,s in Eq. (22) and achieved by the moment-matching scenario generation heuristic proposed by Hoyland et al. [23]. The whole stochastic MILP model, which comprises 564,726 constraints, 19,225 integer variables, and 76,268 continuous variables, is implemented in IBM ILOG CPLEX Optimization Studio v20.1.0. The results of the baseline case with regards to the total mass launched shows that the installation of the space infrastructure is responsible for more than 37% of the total launch mass with in-situ resource utilization (ISRU) facilities and on-orbit depots sharing roughly equal parts. Roughly 170 times more propellant than dry mass is required to support the Martian base over the planning horizon. The tasks are somewhat divided as some vehicles are responsible for the bulk of the cargo while others fetch propellant from the depot. As for infrastructure, ISRU facilities are set up on all planetary satellites, i.e. the Moon, Phobos, and Deimos, while depots are established at L2, LDO, and LMO. And, the capability of depots to store propellant allows to reduce the size of these expensive ISRU plants. To explore the effects of the technological progress on the SC network, sensitivity analyses with regards to the spacecraft’s payload capacity (capQ), its propellant capacity (capP), and the specific impulse (Isp) of the used propulsion system are carried out. Increasing the capQ displays the smallest effects but nevertheless leads to a steady decrease of TLM. Increasing capP takes on similar results but the trend expresses a much steeper decline. Increasing values of Isp have by far the greatest impact on the TLM. The largest effects on infrastructure decisions result, once again, from Isp, for the sizes of both ISRU facilities and depots follow a synchronous exponential decline with Isp increasing. As indicated by these results, the improvement of propulsion systems could be key to actually make ISCs a reality. Moreover, the results also show that increasing availability of ISRU locations substantially improves the efficiency of the ISC.
Finally, the author provides concluding remarks. In this paper, a stochastic multi-stage MILP model is developed that integrates production-distribution and in-space infrastructure allocation decisions in the presence of demand uncertainty. A layered network structure is considered in this model, consisting of a PN and an SN, which are responsible for cargo and propellant supply, respectively. To validated the model, case studies were constructed based on real data on Earth-Mars transfer windows and flight trajectories obtained through NASA’s trajectory browser. The findings show that: 1) a division-of-labor approach is often applied in which some spacecraft carry the bulk of the payload while others fetch propellant from on-orbit depots to supply the entire fleet; 2) spacecraft that launched together from Earth would utilize different transfer windows in order to stagger their arrival times, which effectively allows for smaller sized ISRU facilities and depots in the Mars cluster; 3) advancements in propulsion technology would greatly impact the optimal network design while progress with regards to other spacecraft properties has lesser effects; 4) the availability of ISRU locations strongly influences the optimal solution indicating that the technological capability to manufacture propellant on other celestial bodies is key to an efficient ISC. Overall, the proposed model provides valuable insights and expands our understanding of SC planning by a space logistics perspective.
END