Reservoir computing (RC) is a powerful machine learning module designed to handle tasks involving time-based or sequential data, like tracking patterns over time or analyzing sequences. It is widely used in areas such as finance, robotics, speech recognition, weather forecasting, natural language processing, and predicting complex nonlinear dynamical systems. What sets RC apart is its efficiency—it delivers powerful results with much lower training costs compared to other methods.
RC uses a fixed, randomly connected network layer, known as the reservoir, to turn input data into a more complex representation. A readout layer then analyzes this representation to find patterns and connections in the data. Unlike traditional neural networks, which require extensive training across multiple network layers, RC only trains the readout layer, typically through a simple linear regression process. This drastically reduces the amount of computation needed, making RC fast and computationally efficient. Inspired by how the brain works, RC uses a fixed network structure but learns the outputs in an adaptable way. It is especially good at predicting complex systems and can even be used on physical devices (called physical RC) for energy-efficient, high-performance computing. Nevertheless, can it be optimized further?
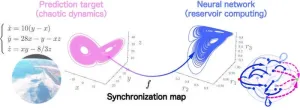
A recent study by Dr. Masanobu Inubushi and Ms. Akane Ohkubo from the Department of Applied Mathematics at Tokyo University of Science, Japan, presents a novel approach to enhance RC. “Drawing inspiration from recent mathematical studies on generalized synchronization, we developed a novel RC framework that incorporates a generalized readout, including a nonlinear combination of reservoir variables,” explains Dr. Inubushi. “This method offers improved accuracy and robustness compared to conventional RC.” Their findings were published on 28 December 2024, in Scientific Reports.
The new generalized readout-based RC method relies on a mathematical function, h, that maps the reservoir state to the target value of the given task, for instance – a future state in the case of prediction tasks. This function is based on generalized synchronization, a mathematical phenomenon where the behavior of one system can be fully described by the state of another. Recent studies have shown that in RC, a generalized synchronization map exists between input data and reservoir states, and the researchers used this map to derive the function h.
To explain this, the researchers used Taylor’s series expansion which simplifies complex functions into smaller and more manageable segments. In contrast, their generalized readout method incorporates a nonlinear combination of reservoir variables, allowing data to be connected in a more complex and flexible way to uncover deeper patterns. This provides a more general, complex representation of h, enabling the readout layer to capture more complex time-based patterns in the input data, improving accuracy. Despite this added complexity, the learning process remains as simple and computationally efficient as conventional RC.
To test their method, the researchers conducted numerical studies on chaotic systems like the Lorenz and Rössler attractors—mathematical models known for their unpredictable atmospheric behavior. The results showed notable improvements in accuracy, along with an unexpected enhancement in robustness, both in short-term and long-term predictions, compared to conventional RC.
“Our generalized readout method bridges rigorous mathematics with practical applications. While initially developed within the framework of RC, both synchronization theory and the generalized readout-based approach are applicable to a broader class of neural network architectures,” explains Dr. Inubushi.
While further research is needed to fully explore its potential, the generalized readout-based RC method represents a significant advancement with promise for various fields, marking an exciting step forward in reservoir computing.
***
Reference
Title of original paper: Reservoir computing with generalized readout based on generalized synchronization
Journal: Scientific Reports
DOI: https://doi.org/10.1038/s41598-024-81880-3
About The Tokyo University of Science
Tokyo University of Science (TUS) is a well-known and respected university, and the largest science-specialized private research university in Japan, with four campuses in central Tokyo and its suburbs and in Hokkaido. Established in 1881, the university has continually contributed to Japan's development in science through inculcating the love for science in researchers, technicians, and educators.
With a mission of “Creating science and technology for the harmonious development of nature, human beings, and society," TUS has undertaken a wide range of research from basic to applied science. TUS has embraced a multidisciplinary approach to research and undertaken intensive study in some of today's most vital fields. TUS is a meritocracy where the best in science is recognized and nurtured. It is the only private university in Japan that has produced a Nobel Prize winner and the only private university in Asia to produce Nobel Prize winners within the natural sciences field.
Website: https://www.tus.ac.jp/en/mediarelations/
About Associate Professor Masanobu Inubishi from Tokyo University of Science
Masanobu Inubushi is currently an Associate Professor at the Tokyo University of Science, Japan. He obtained his undergraduate degree in 2008 from the Tokyo Institute of Technology, Japan. He then obtained his PhD in Mathematics from the Research Institute for Mathematical Sciences (RIMS) at Kyoto University in 2013. After working at NTT, Communication Science Laboratories from 2013-2018, he joined Osaka University as Assistant Professor in 2018. Dr. Inubushi has over 25 published research articles that have been cited over 400 times. His research interests include fluid mechanics, chaos theory, mathematical physics, and machine learning.
Funding information
This work was partially supported by JSPS Grants-in-Aid for Scientific Research (Grants No. 22K03420, No. 22H05198, No. 20H02068, and No. 19KK0067).
END