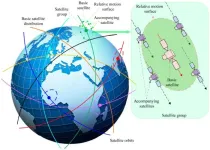
First, satellites in the mega constellation are categorized and the constellation design based on different satellite division is proposed. Satellites in the mega constellation are divided into 2 types, namely, the basic satellites and the accompanying satellites. All basic satellites that are surrounded by accompanying satellites are evenly distributed globally, and they have the same subsatellite trajectory. A basic satellite and its accompanying satellites are defined as a satellite group. The constellation is composed of many satellite groups, as shown in Fig. 1.
As for basic satellites, the semimajor axis a of regression orbit can be numerically solved considering (1) that regression orbit requires a satellite flies R times around Earth in D days and (2) that the influence of J2 perturbation force of an orbit is considered. Assuming that the ground coverage width of a satellite group is d, the number of basic orbital plane is Nt = ceiling(2πRe/d) where ceiling(⋅) is the round up function. Assuming that the maximum response time to complete Earth observation mission required by the user is mt and the orbital plane is evenly divided according to the orbital period T, the number of basic satellites in each orbital plane is Nn = ceiling(T/mt). Based on above analysis, input the i, e, and ω of the constellation and Q = R/D, then the basic satellites constellation is designed.
As for accompanying satellites, they have the semimajor axis with basic satellites. According to the Clohessy-Wiltshire equation, the relative motion trajectory between the basic satellites and the accompanying satellites is an ellipse. Then, considering that the position vectors at the initial time and T/2 relative to the basic satellite is oppositive, the orbital elements of the first accompanying satellites can be solved. Assuming that the imaging width of a single satellite is sd, the number of accompanying satellites in a satellite group is Na = ceiling(d/sd - 1). Divide the trajectory of the first accompanying satellite relative to basic satellite orbital coordinate system in chronological order, extract the position vectors of all equal points under the orbital system, and use these as the position vectors of other accompanying satellites under the basic satellite orbital system at initial time.
Combining the basic and accompanying satellites’ orbits, the configuration of mega constellation is obtained.
Fig. 1. Orbital distribution of LEO mega constellation.
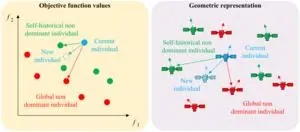
Then, the orbit parameters of satellite and its companions are set as initial values, and the precise orbits under the High Precision Orbit Propagator model are solved in the neighborhood by using the Nondominated Sort Particle Swarm Optimization algorithm. Transform the orbital elements of any basic satellite into position and velocity information, which is recorded as {pxpq, pypq, pzpq, vxpq, vypq, vzpq}. Add an increment to build their neighborhood, which can be expressed to {Δpxpq, Δpypq, Δpzpq, Δvxpq, Δvypq, Δvzpq}. The optimization variable of accompanying satellite orbit is the position and velocity increment of all basic satellites. The optimization objective f1 for the basic satellite configuration is to minimize the absolute difference between the ascending and descending nodes of any basic satellite bspq in cycle i, and the ascending and descending nodes of bs1q as much as possible. The optimization objective f2 of the accompanying satellite is to keep the relative position as close as possible under the basic satellite orbit system at multiple subsequent motion periods. Optimization iteration process involves continuously approaching the Pareto front. In practice, find all nondominant solutions of the initial individual as the optimal solution set. Calculate 2 optimization objectives of everyone in sequence, and use the nearest global nondominated individual and own historical nondominated individual as learning objects. Update individual optimization variables and variable increments based on population information, individual experience, and self-inertia, as shown in Fig. 10. Then calculate the f1 and f2 of newly generated individuals again, and regenerate the global Pareto front and individual historical Pareto front. After a fixed number of cycles or objective function is less than the threshold, the iteration ends and the global Pareto front can be obtained. At this point, the final constellation configuration can be selected based on user preferences or linear superposition of f1 and f2.
Fig. 10. Individual update process.
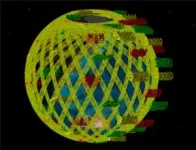
Finally, the correctness of the configuration design method is verified by numerical simulation. In the simulation, set the constellation orbital inclination as 66°, eccentricity as 0, argument of perigee as 0, simulation time as 1 d, set regression coefficient Q = 15, initial ascending node as 0, initial MA as 0, imaging width of a satellite group as 1500 km, imaging width of single satellite as 140 km, and maximum working time of single satellite to orbit single circle as 35 min. During the optimization, it can be observed that the approximation speed of the Pareto front in the first 100 generations is extremely fast. As the number of iteration increases, the variation of the Pareto front gradually decreases and eventually becomes stable. In the final generation of nondominated solutions, we select the individual of f1 = 1.981 and f2 = 9516.482 as the final solution, and the constellation configuration is shown in Fig. 15. The constellation has a total of 891 satellites, of which 81 basic satellites are evenly distributed, with 10 accompanying satellites evenly distributed around each basic satellite. A total of 810 accompanying satellites can achieve collaborative observation of any position outside the polar region within 35 min.
Fig. 15. Final LEO mega constellation configuration.
END